Out of curiosity, I ran two tests on the publicly available RSA keys within the sks keyserver system. First, can it be factored by the first 1000 primes? Second, do any pairs of keys share a common factor?
The results -- within the roughly 1.9 million RSA moduli available as a key or subkey:
1. Only one pair shared a common factor - these are two v3 keys with 1024-bit moduli (and have also expired quite a few years back.)
2. There were 41 valid keys with an RSA subkey divisible by a small prime. However, the remaining number is still composite, so perhaps it is some glitch in the prime-generation component of the code.
How I ran the tests
I downloaded one of the daily database dumps available from one of the sks keyservers. After skipping over any key that could not be fully parsed, I extracted any RSA modulus from the primary or subkey, together with the primary key fingerprint.
Next I removed RSA duplicate moduli within the same key - about one out of every 150k keys seem to reuse the modulus within a subkey.
At this point, I ran the first test. This finds the gcd of each modulus with the product of the first 1000 primes. We'd like the gcd to be 1, otherwise we've found a low-prime factor for the modulus.
This step found 165 distinct moduli that had low-prime factor(s), of which 41 were fully valid keys. However, all of these 41 keys had moduli that remained composite after factoring by the small prime.
I emailed 8 people in these keys (who had a reasonable number of signatures on their keyring.) One replied saying that he'd used gnupg on Fedora to generate the key, the other that he'd used the commercial PGP product - both some years back. I passed on the info to the gnupg maintainer as well as to Symantec.
Next, I removed duplicates across keys -- 163 moduli were reused across different keyrings. I did a spot-check on about 10% of them, and it appears to belong to people recreating v4 keys with the same moduli but with different creation timestamps (which changes the key fingerprint.)
At this point, I ran Nadia Heninger et. al.'s all-pairs GCD test on the remaining 1,901,662 moduli. It found one pair of moduli with a shared factor - it belongs to a pair of 1024-bit v3 keys that have long since expired.
Miscellania
If you were curious, this is the number of moduli of different lengths that I found within keys/subkeys.

Just for fun, I plotted a histogram of the first 11 bits of RSA moduli that were exactly 2048 bits long (the most common size.) The leading bit is always going to be 1, so the histogram actually starts from 100000....
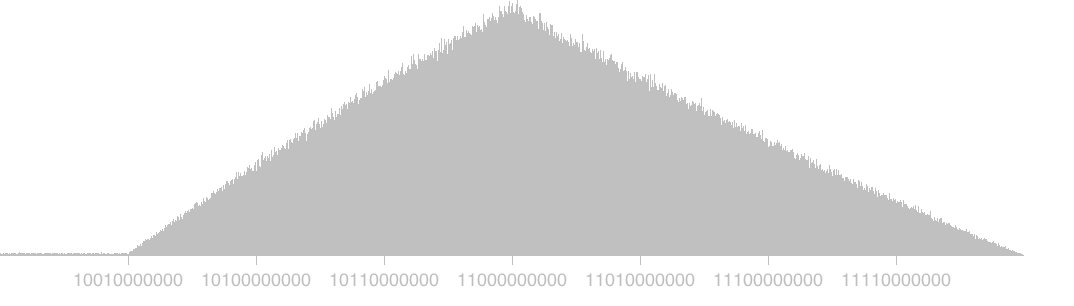
This looks weird, because you might expect this to be uniform. But after much head scratching and code re-checking, here's my explanation of the distribution that I actually see. Please do feel free to enlighten me about mistakes, of course!
These numbers are the product of two uniformly distributed 1024-bit primes, so (to a first approximation) it is the product of two uniform distributions. This turns out to be a slightly nasty piecewise continuous log function that looks like a saw-tooth.
But the sawtooth doesn't begin all the way to the left - instead there is a flat section with very few moduli. I believe this is the result of the way gnupg (and perhaps other widely used PGP tools) generate primes.
If you ask gnupg to generate a 2048 bit modulus, it starts by finding two 1024 bit primes. To find such a prime, it starts to generate random 1024 bit numbers with their first two bits set to 1, until one such number passes a number of primality tests. Why does it always set their first two bits to 1? Because this guarantees their product will never be smaller than 2048 bits.
A bit of algebra shows why -- to generate a 2n bit composite number out of two n-bit primes, gnupg picks primes that that are at least 2^(n-1) + 2^(n-2).
So its product is at least (2^(n-1) + 2^(n-2))^2, which after some algebra you can reduce to
2^(2n-1) + 2^(2n-4)
But this also means that any gnupg generated RSA modulus will be larger than this number. To put it another way, gnupg will always generate a modulus that's larger than 1001000... and this exactly matches the "flat" region at the beginning of the histogram. I believe the moduli in the initial flat section probably come from programs that don't use the logic of setting the first 2 bits of their primes to 1.